接雨水 是 Leetcode 上的一道经典的算法题目,它可以用很多种方法来解决,可以很好的考察做题者的思维方式。
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
比如我们有一串柱子的高度数组 [2, 1, 3, 1, 0, 1, 2],我们可以画出对应的表示图。
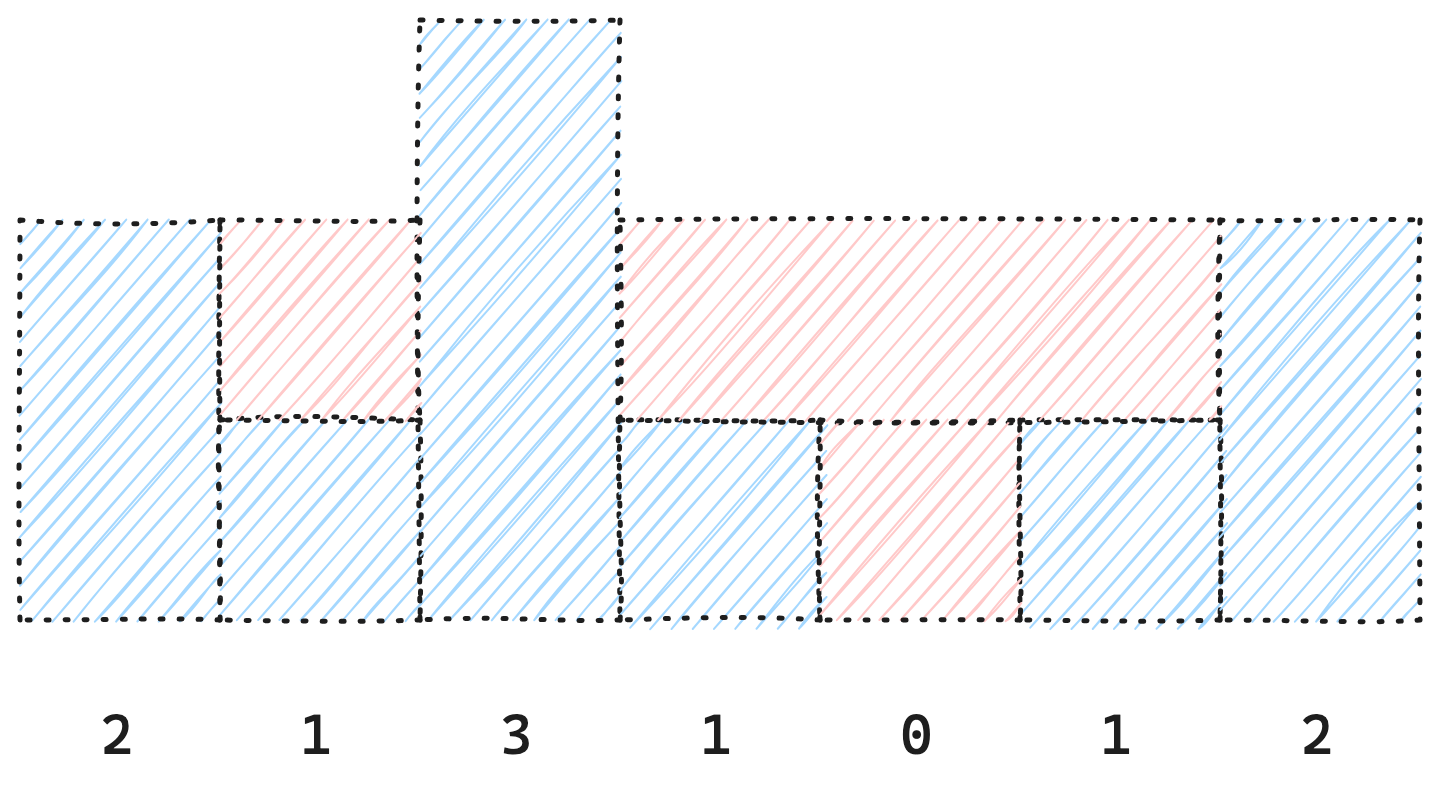
可以看出 红色区域 就是我们可以盛放的雨水数目。
解题思路
首先我们可以很快的想出一种最简单的办法就是遍历高度数组,当我们遍历到当前的柱子的时候,向左 和 向右 找到当前柱子分隔的左区间 [0, i] 和右区间 [i, n) 最大值,然后根据木桶效应,选取两者之间的 最小值 减去当前柱子的高度就是当前柱子可以盛放的水的数目。
func trap(height []int) int {
n := len(height)
res := 0
for i, v := range height {
maxLeft, maxRight := v, v
for l := 0; l < i; l++ {
maxLeft = max(height[l], maxLeft)
}
for r := i; r < n; r++ {
maxRight = max(height[r], maxRight)
}
res += min(maxLeft, maxRight) - v
}
return res
}但是这个算法是 $$O(n^{2})$$ 的,对于大量的数据会出现超时操作。
针对超时问题,我们需要改进我们的算法。我们可以进行一次遍历找到 最高的柱子,然后可以看成左区间 [0, i) 一定是 递增 到最高的柱子,右区间 (i, n) 是从最高的柱子开始 递减。所以 从头 开始遍历左区间可以找到 目前的最大值,如果遍历到的柱子不是最大值,说明可以和左区间的目前最大的柱子形成一个凹槽来盛水。相反,对于右区间我们可以从 尾部 反向遍历区间,这样就是一个递增的过程,同样可以用左区间的方式来处理。这样算法时间复杂度就是 $O(n)$。
func trap(height []int) int {
n := len(height)
res := 0
peak, peakIndex := 0, 0
for i, v := range height {
if peak < v {
peakIndex = i
peak = v
}
}
maxLeft := 0
for _, v := range height[:peakIndex] {
if maxLeft < v {
maxLeft = v
} else {
res += maxLeft - v
}
}
maxRight := 0
for i := n - 1; i > peakIndex; i-- {
if maxRight < height[i] {
maxRight = height[i]
} else {
res += maxRight - height[i]
}
}
return res
}我们还可以使用单调栈来做这题,我们可以建立一个单调递减栈,当有柱子的高度 大于 当前 栈顶 的柱子高度,说明可以形成一个凹槽来盛放雨水。这样我们就可以计算这个凹槽的大小从而计算可以盛放多少雨水。
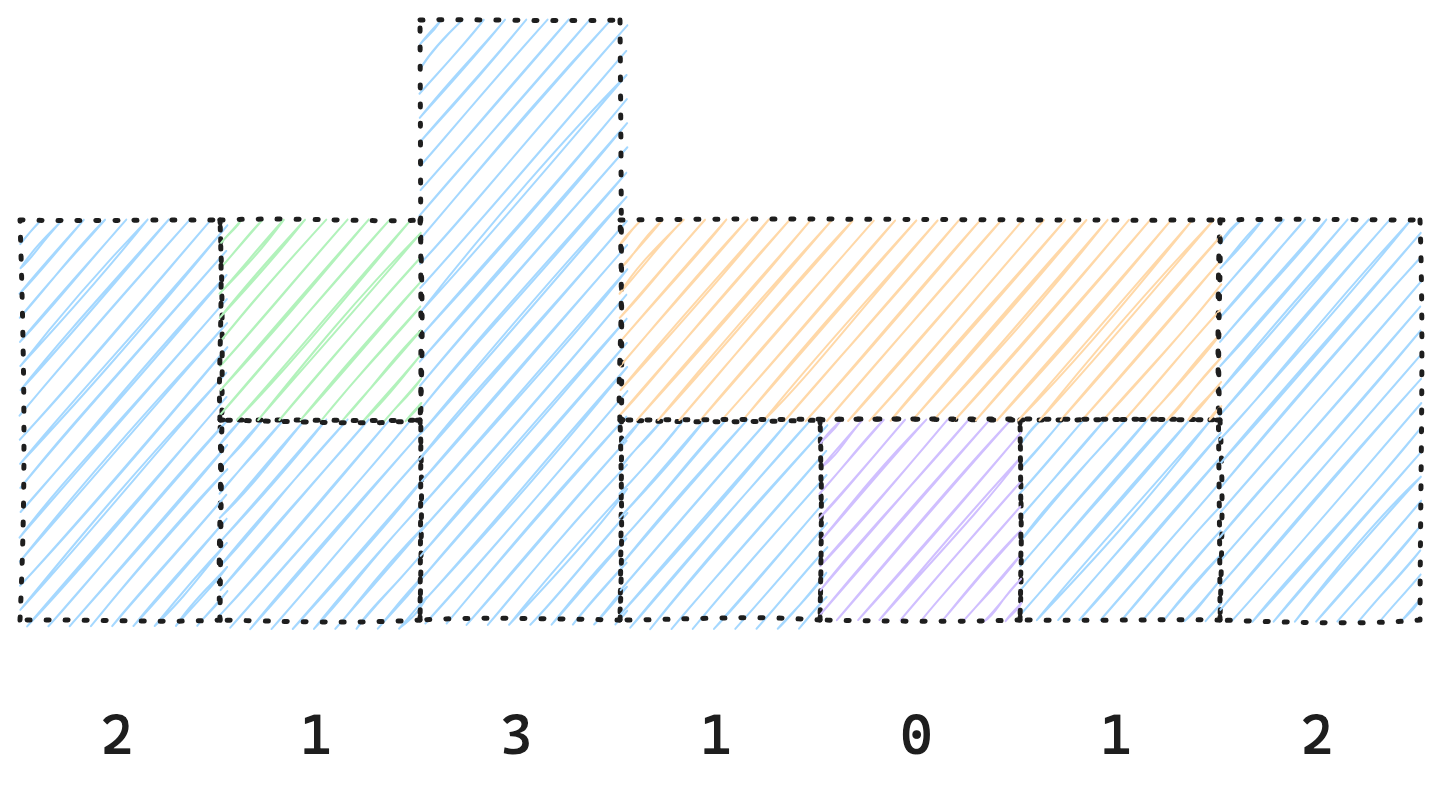
对于绿色的凹槽,单调递减栈中存放的是:
2 1,当3过来的时候说明可以和2 1 3形成一个凹槽。对于紫色的凹槽,单调栈中当时存放的是:
3 1 0,当1过来的时候说明可以和1 0 1形成一个凹槽。对于黄色的凹槽,单调栈中当时存放的是:
3 1 1,当2过来的时候说明不可以和1 1 2形成一个凹槽,将栈顶的1弹出。这时候就可以和3 1 2形成一个凹槽。
func trap(height []int) int {
st := make([]int, 0)
res := 0
for i := 0; i < len(height); i++ {
// height[st[len(st)-1]] <= height[i] 也可以
for len(st) != 0 && height[st[len(st)-1]] < height[i] {
t := st[len(st)-1]
st = st[:len(st)-1]
if len(st) != 0 {
res += (min(height[i], height[st[len(st)-1]]) - height[t]) * (i - st[len(st)-1] - 1)
}
}
st = append(st, i)
}
return res
}